Rediscovering the Randwalk
It was over 7 years ago that I solved a problem for my International Bacclaureate extended essay. The problem is as follows:
3/4/20. A particle is currently at the point (0, 3.5) on the plane and is moving towards the origin. When the particle hits a lattice point (a point with integer coordinates), it turns with equal probability 45° to the left or to the right from its current course. Find the probability that the particle reaches the x-axis before hitting the line y = 6 USA (Mathematical Talent Search).
The fact that I even wrote the essay in mathematics (instead of history) is surprising since I had attended an Upper Canada College class on writing extended essays, and I had already figured out the crux of my history thesis: that the Byzantines were undone by economic stupidity. But my last year in high school was an important year for me in math. Although I took no formal courses in it, I was invited to write the Canadian Math Olympiad, which despite having flunked, placed me in a fairly small group of people.
I always had a fascination with probability and the problem above was the most interesting I had seen. Unlike many difficult problems in mathematics, the problem was down to earth. You could write a program that drew the pretty graphs, and you could run it enough times to find the approximate answer. The analytical solution was interesting as well, requiring for a few non-obvious equations to be written and solved.
The real intrigue though has to do with patterns. Mathematicians are obsessed with patterns. The computer program showed that there was an oddly kinked curve for the general solution (the solution for the particle between $y=0$ and $y=N$). It appeared as though the solution was smooth on an interval of 4, but non-smooth on an interval of 2. Furthermore, it became quite clear that the solution was asymptotic to 1/2, but the path down to 1/2 was not fitted to a simple function like an exponential function.
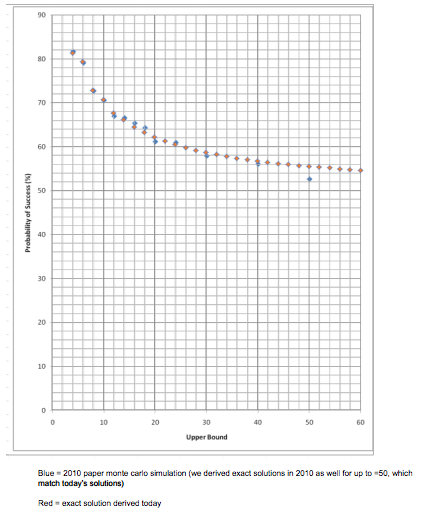
In 2010, the paper that was submitted to the IB program for grading did not find the reason for the non-smooth nature, at least not mathematically (subconsciously, I think I knew what the reason was, though I never spelt it out in the paper). What I presented was a method for solving the problem using N - 1 linear equations. This is also not obvious and at the time provided precise analytical solutions (non-simulated) for every N but a computer was needed to take inverses of large matrices. I had always known that the answer was incomplete. In the original essay, I wrote that “our current method has a heavy reliance on technology. In the future, I’d like to explore to find perhaps an even more direct method of attaining the answer.”
The following year, I wrote the paper Skunk which was also based on probability with my professor. Even then I was wildly curious about this problem that I had left open from the previous year. I had tackled it with Gaussian elimination, a new concept at the time, but no headway was made. I even sent the 2010 essay to my professor to see if he had any ideas. I am unsure if he ever read it. During Christmas of 2012, prior to leaving for Paris, I once again tackled the problem. By then I had learnt the key mathematical theories of undergrad but still could not figure out the problem.
The breakthrough occurred in the last month. I had been trying to revisit some old problems, including the old COMM 341 case which I recently published on my blog because of its connection with airline overbooking. The key observation was that the problem could be reduced to a recursion with a static number of terms for every N. In other words, one could reduce a problem with N - 1 variables into 4 variables, no matter how big the problem was. The math required to do this should have been obvious by 2012, but it took until 2017 for it to show itself. It took a few days to work out all the numbers, including one night that involved girl issues (not mine, for once) and GMAT preparation (also not mine). But the equations revealed an answer. It is still unbelievably complicated but it can be written down by hand. The answer does not become more complicated for higher N, which is an important quality for a good answer. The answer also had different equations for odd and even N/2, which explains the pattern from 2010 that the curve was smooth on intervals of 4 but not 2.
\[g_{n} = - v^{N}v^{- n} + v^{n}\] \[r = \frac{8\left( g_{1} - g_{0} \right) - 4\left( g_{3} - g_{2} \right) - \left( g_{2} - g_{1} \right)}{- 3}\] \[d = \frac{- 3}{16g_{0} - 8g_{2} - 2g_{1} - 18r - 3Nr}\] \[b = dr\] \[a = \frac{1}{2} - \frac{N}{2}b\] \[c = - v^{N}d\] \[P_{n} = \left\{ \begin{matrix} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0,\ \ \ n \leq 0 \\ a + nb + cu^{n} + dv^{n},\ \ 1 \leq n \leq N - 1 \\ 1,\ \ n \geq N \\ \end{matrix} \right.\\]$n + 1 - 2i \leq n - 1$. The solution is as follows:
$n$ odd
\[G_{n} = \frac{2^{- 1} - 2^{- \frac{n + 1}{2}}}{1 - 2^{- 1}}a + \left( \frac{2^{- 1}\left( n - 1 \right) - 2^{- \frac{n + 1}{2}}\left( 0 \right)}{1 - 2^{- 1}} + \frac{2^{- 2}\left( - 2 \right) - 2^{- \frac{n + 1}{2} - 1}\left( - 2 \right)}{\left( 1 - 2^{- 1} \right)^{2}} \right)b + \frac{2^{- 1}\left( - v^{N}v^{- \left( n - 1 \right)} \right) - 2^{- \frac{n + 1}{2}}\left( - v^{N}v^{0} \right)}{1 - 2^{- 1}v^{- 2}}d + \frac{2^{- 1}v^{n - 1} - 2^{- \frac{n + 1}{2}}v^{0}}{1 - 2^{- 1}v^{2}}d\]$n$ even
\[G_{n} = \frac{2^{- 1} - 2^{- \frac{n + 2}{2}}}{1 - 2^{- 1}}a + \left( \frac{2^{- 1}\left( n - 1 \right) - 2^{- \frac{n + 2}{2}}\left( - 1 \right)}{1 - 2^{- 1}} + \frac{2^{- 2}\left( - 2 \right) - 2^{- \frac{n + 2}{2} - 1}\left( - 2 \right)}{\left( 1 - 2^{- 1} \right)^{2}} \right)b + \frac{2^{- 1}\left( - v^{N}v^{- \left( n - 1 \right)} \right) - 2^{- \frac{n + 2}{2}}\left( - v^{N}v^{1} \right)}{1 - 2^{- 1}v^{- 2}}d + \frac{2^{- 1}v^{n - 1} - 2^{- \frac{n + 2}{2}}v^{- 1}}{1 - 2^{- 1}v^{2}}d\]The significance of this problem is that this is the reason for the title of my blog (not because of the movement of stock prices, though they’re all random walks). See http://randwalk.com/about-this-blog/ for some lovely computer generated images. Unfortunately the solution is still not simple but it is unclear if a simpler expression can be formed.
To see the original essay: www.randwalk.com/s/Extended-Essay-42.pdf
To see the new essay, please contact me.