Should you buy into a Jackpot of $868m?
In a country where social mobility is promised but is exceedingly rare, it is not surprising that lottery prizes run to extremes. This week, a stupid amount can be won: $868 million USD. That raises the question of whether it is ever beneficial to play the lottery. That is if there is ever a positive expected value. The answer is a complicated one, and so makes for a good blog article.
The Powerball game, the format of the largest lottery event in history, involves two parts. First, you must choose five distinct numbers from 1 to 69, and then choose one number (the “Powerball”) from 1 to 26. To win the prize, you must choose the five numbers correctly (without consideration of order), as well as the Powerball number correctly.
The odds are not difficult to calculate. They are shown here http://www.powerball.com/pb_home.asp. They can be calculated using “lottery probability”. In the first part of Powerball, there are five numbers drawn from 69 balls. The number of ways to do this is written as “69 choose 5” or on excel combin(69,5). It is a mathematical formula that can be derived either using factorials or using pascal’s pyramid. But most simply, it is done on Excel. The answer is 11,238,513. Then multiply by 26 for the Powerball. The result is 292,201,338, for which there is only one winning combination, and so the odds are 1 in 292,201,338.
The winning combinations increase for the lower tier prizes. To choose 4 correct numbers, there are
\[\begin{pmatrix} 5 \\ 4 \\ \end{pmatrix}\begin{pmatrix} 69 - 5 \\ 5 - 4 \\ \end{pmatrix}\]ways, and so on. To explain this quickly, there are 5 choose 4 ways to choose the correct numbers and 64 choose 1 ways to choose the incorrect numbers, and any combination of the correct and incorrect numbers will result in a certain tier of prize. To adjust for the Powerball, multiply by 25 if the Powerball is to be incorrect, and 1 if it is to be correct. That gives you the odds on the website.
Quickly look at the expected value at each tier of prize. For now, we exclude the Jackpot because that number changes depending on the number of winning tickets.
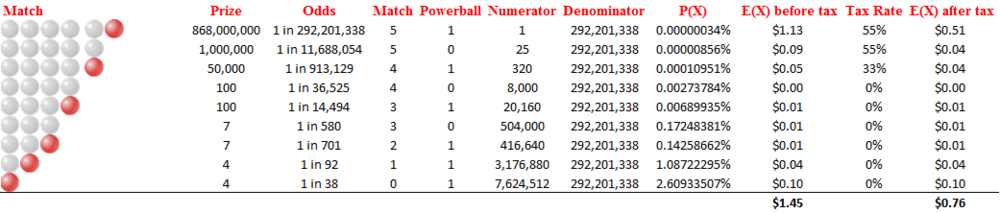
We notice that, excluding the jackpot, the expected return is only 32 cents on a $2 ticket. We make the assumption that any winnings $100 or less will not be taxed, with increasing tax rates for higher amounts. That results in an after tax return of 25 cents. It is interesting to also notice that the expected returns diminish as odds decrease. I would think this is to create more winners, which leads to higher future sales.
Now, we focus on the Jackpot since that is clearly where most of the expected return will come from. This expectation will depend on the number of co-winners. In the event that you have the Jackpot winning ticket, the number of other winners will follow a binomial distribution with n = number of tickets potentially with your winning number and p = 1/292,201,338, the odds of winning. Now we must calculate the expected value for a given n.
We need the quantity
\[E\left( \frac{J}{k + 1} \right)\]where $\mathbf{J}$ = the jackpot prize, and $\mathbf{k}$ = the number of other winning tickets.
\[E\left( \frac{J}{k + 1} \right) = \sum_{k = 0}^{}\left( \frac{J}{k + 1} \right)\begin{pmatrix} n \\ k \\ \end{pmatrix}p^{k}\left( 1 - p \right)^{n - k}\]Writing combinations with factorials,
\[\begin{pmatrix} n \\ k \\ \end{pmatrix} = \frac{n!}{k!\left( n - k \right)!}\]we get
\[E\left( \frac{J}{k + 1} \right) = J\sum_{k = 0}^{}{\frac{n!}{(k + 1)!\left( n - k \right)!}p^{k}\left( 1 - p \right)^{n - k}}\]which rearranges as
\[E\left( \frac{J}{k + 1} \right) = J\sum_{k = 0}^{}{\frac{n!}{(k + 1)!\left( n - k \right)!}p^{k}\left( 1 - p \right)^{n - k}} = \frac{J}{p\left( n + 1 \right)}\sum_{k = 0}^{}{\frac{(n + 1)!}{(k + 1)!\left( (n + 1) - (k + 1) \right)!}p^{k + 1}\left( 1 - p \right)^{(n + 1) - (k + 1)}}\]Here, it will become clear why we rearranged the equation. This complicated formula is almost always going to be intractable. Except, in this case, we notice that the summation is just of the probability densities of a $Binom(p,\ n + 1)$. The sum across the space of a probability density is always 1, so we can simplify the summation. More precisely, the summation is sum of the pdfs of $Binom(p,\ n + 1)$ less the pdf when $k = - 1$. Thus
\[E\left( \frac{J}{k + 1} \right) = \frac{J}{p\left( n + 1 \right)}\left( 1 - \left( 1 - p \right)^{(n + 1)} \right)\]which is the expected winning given you have a winning ticket. The probability of having a winning ticket is $p$, and assuming a tax rate of 55%, your expected winnings from the Jackpot tranche is
\[\frac{J}{n + 1}\left( 1 - \left( 1 - p \right)^{\left( n + 1 \right)} \right)(1 - 0.55)\]Thus the total expected return in dollars is
\[0.25474 + \frac{868,000,000}{n + 1}\left( 1 - \left( 1 - \frac{1}{292,201,338} \right)^{n + 1} \right)\left( 1 - 0.55 \right)\]All you need to do is guess how many people have tickets that are capable of winning. Apparently 500 million tickets have already been sold, meaning it is likely that 1bn will be purchased by Wednesday night. Assume you pick a number that is obscure – that people wouldn’t pick themselves. Something with a lot of 13’s, maybe. 70% of tickets are sold on computers, using random number generators. So let’s assume there are 700 million tickets that can be similar to yours. Putting that into the equation gives an E(X) of $0.76 on a $2.00 ticket. I guess it could be worse.
Disclaimer: Randwalk is currently the holder of $10 worth of tickets and will benefit from readers not purchasing tickets, which would decrease n and increase $E\left( \frac{J}{k + 1} \right)$. The tickets have been capitalized at $3.8, the rest amortized over the life of the ticket.