A Comprehensive Definition of Happiness
In this article, I improve on my previous attempts to define happiness. I am convinced that happiness is reconciliation between expected and actual results. However, the relationship between the two has been ill-defined. But, let us try.
For simplicity, we will assume there is a linear relationship. That is, happiness is exactly the difference between expected and actual results:
ϵ=Y-X
Here, ϵ is happiness, $Y$ is actual results and X is expected results. Taking Y to be a function of X (since Y happens after X)
Y=X+ϵ

This gives an equation for a linear regression through the origin with beta = 1. Happiness is the error term. Three conditions must hold. ϵ must be normally distributed, be independent sample-to-sample and have constant variance. These are mostly reasonable. For example, constant variance verifies that people of all income levels are similarly happy. Independence sample-to-sample means day-to-day variations can be rocky, another generally accepted consequence of life. That ϵ is normally distributed, however, is less substantiated. Kurtosis (fat tails, i.e. bi-polar) and skewness (like the perennially disappointed French) are likely characteristics of happiness. However, for ease of analysis, we will assume ϵ is normal.
Implication 1: The goal should be the decrease standard deviation.

σ = 10, μ = 0
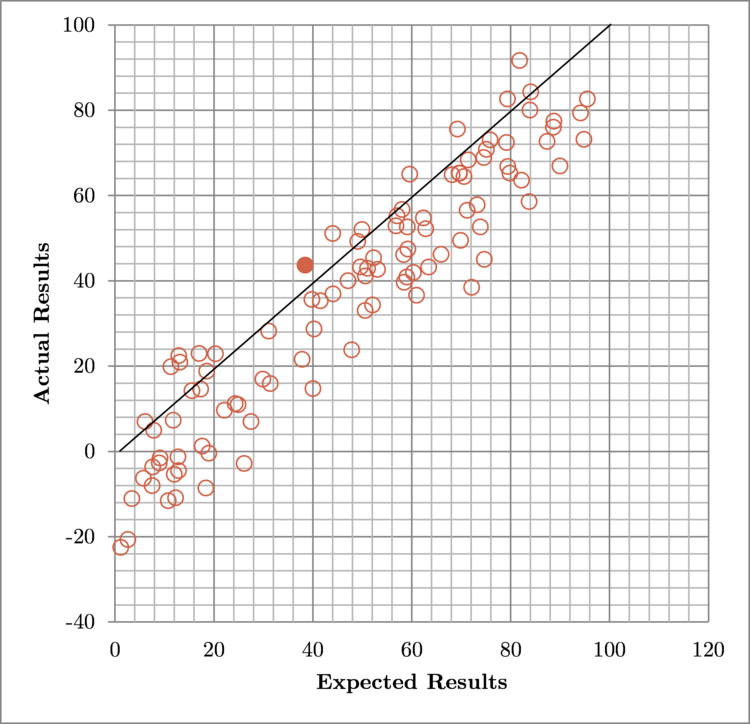
σ = 50, μ = 0
Implication 2: Learn to predict results more accurately
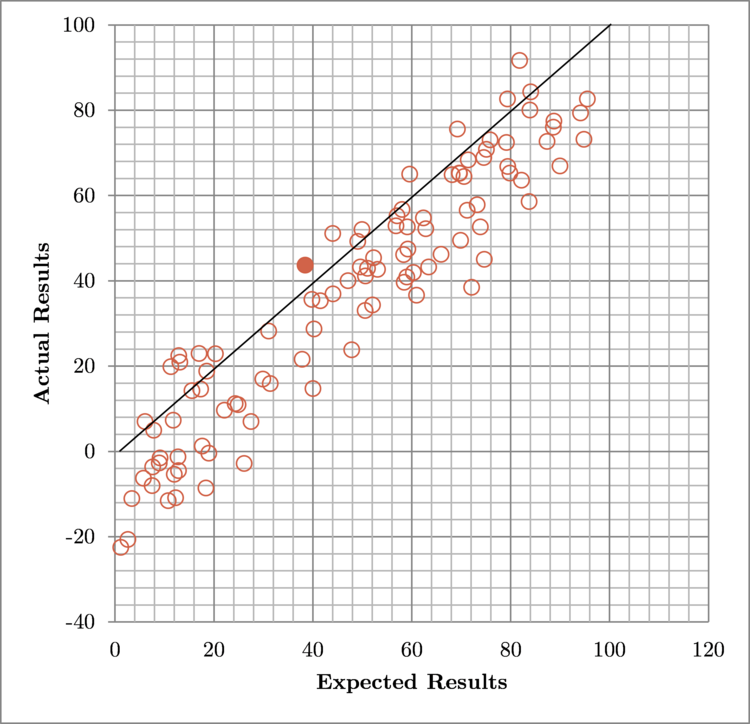
σ = 10, μ = -10
Overly-optimistic predictions result in unhappiness
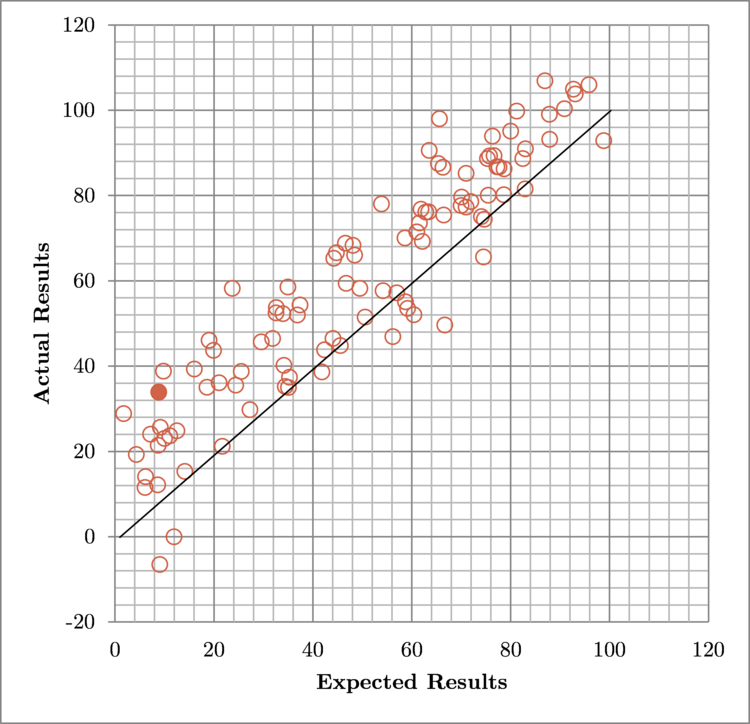
σ = 10, μ = +10
Overly-pessimistic predictions result in happiness